HOME＞よみもの＞ボイルシャルルの法則

ボイルシャルルの法則

空気圧で基本となる。ボイルシャルルの法則ですが、ネット上を見渡しても簡単な記述のサイトか専門用語が一杯の難しいサイトしかない為、解りやすく且つ詳しく説明いたします。



（１）空気の状態変化
気体には、圧力・体積・温度の三要素で一定の関係があり、このうち２要素が決まれば残りの１要素は必然的に決定されます。空気の場合にも３要素で表せ三要素間の関係を表す式を「状態式」といいます。
状態の変化は「等温変化」「断熱変化」に大別され、空気と外部との熱の出入りが自由な状態での変化を「等温変化」、熱の出入りが全くない状態での変化を「断熱変化」といいます。


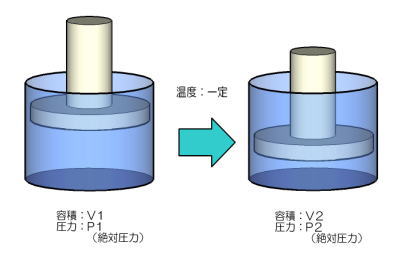
（２）ボイルの法則
圧力及び体積が一定量の空気を温度を保ったまま圧縮または膨張させた場合。次の式が成り立ちます。

変化前の圧力×変化前の体積＝変化後の圧力×変化後の体積
Ｐ１×Ｖ１＝Ｐ２×Ｖ２

温度が一定であれば、一定量の気体の圧力と体積の積は常に一定であり、これを「ボイルの法則」といいます。



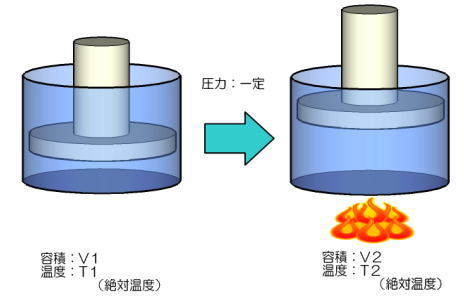
（３）シャルルの法則
体積及び絶対温度が一定量の空気の圧力を一定に保ったまま加熱または冷却させた場合、次の式が成り立ちます。

変化前の絶対温度 ＝ 変化前の体積
変化後の絶対温度 変化後の体積

Ｔ１ ＝ Ｖ１
Ｔ２ Ｖ２

圧力が一定であれば、一定量の空気の体積は絶対温度に正比例の関係であり、これを「シャルルの法則」といいます。


（４）ボイル・シャルルの法則
一定量の気体の圧力や温度を変えると体積が変わることは「ボイルの法則」と「シャルルの法則」から知ることが出来るが、圧力、温度、体積の三要素が共に変化する場合、これら２つの法則を１つにまとめたものが必要となり、これが「ボイル・シャルルの法則」となります。

圧力×体積＝気体の重量×ガス常数×絶対温度
ＰＶ＝ＧＲＴ

「ガス常数」は気体の種類により定まる数値で空気の場合は２９．７kgf･m/kgf･Kである。
この式を「状態式」や「ボイル・シャルルの式」といいます。


（５）等温変化の場合
一定量の気体の状態変化が一定温度のもと行われる変化を「等温変化」といい圧力と体積が一定量の期待が温度変化無しに変化する場合「ボイル・シャルルの法則」から次の式が成り立ちます。

Ｐ１×Ｖ１＝Ｇ×Ｒ×Ｔ
Ｐ２×Ｖ２＝Ｇ×Ｒ×Ｔ
となり
Ｐ１／Ｐ２＝Ｖ２／Ｖ１
の関係が成り立ちます。

圧力は体積に反比例することが証明されます。これは「ボイルの法則」そのものであり温度変化を伴う場合にも同様にして次の式が成り立ちます。

Ｐ１×Ｖ１＝Ｇ×Ｒ×Ｔ１
Ｐ２×Ｖ２＝Ｇ×Ｒ×Ｔ２
となり

Ｐ１×Ｖ１ ＝ Ｐ２×Ｖ２
Ｔ１ Ｔ２
の式がなりたちます。

（６）断熱変化の場合
一定量の気体が外部との熱の出入りが全くない状態で圧力や体積が変化することを「断熱変化」といい、気体が膨張し体積が増加すれば、外部に対して仕事をしたことになるが、外部との熱の出入りがない状態で行われると気体の持つエネルギーの一部が消費され、気体の温度が低下し「等温変化」の場合に比べ圧力は低くなります。
逆に圧縮され体積が減少するとエネルギーが気体の内部に蓄えられたことになり、「等温変化」に比べ圧力の変化は大きくなります。

一般的にエアーコンプレッサでの空気を圧縮する場合や、エアータンクに蓄えられた空気を一気に放出する場合は変化が短時間で行われるため「断熱変化」とみなします。

断熱変化の場合の圧力の体積は次の式で表せます。
圧力×比容積×断熱比＝一定
Ｐ×ｖ×ｋ＝一定


比容積ｖ： １
（ Ｐ ）
ＲＴ

断熱比ｋ： 定圧比熱
定積比熱

であり
Ｐ１×ｖ１×ｋ＝Ｐ２×ｖ２×ｋ
となります。

断熱比ｋは断熱変化を表す指数で「断熱指数」ともいい、空気の場合は１．４となります。温度との関係式は「シャルルの法則」から次の式で表せます。
Ｔ１ ＝ （ Ｐ１ ） k-1
k		 ＝ （ ｖ２ ） k-1
Ｔ２ Ｐ２ ｖ１